Consider the following polygon \(P\):
A polygon.
The Convex Cover problem seeks to cover \(P\) with the fewest convex polygons that lie within \(P\). Here, the minimum number of convex polygons required is 3:
An optimal convex cover of our polygon.
Convex Cover is a fundamental problem in Computational Geometry; it was first studied in the late 60s [1] and in 2003 an \(\mathcal{O}(\log{n})\)-approximation (and and APX-Hardness reduction) was discussed in [2] (\(n\) is the number of vertices of \(P\)). This algorithm is extremely slow (runtime in the order of \(n^{29}\)). Recently, in [3], Abrahamsen showed that Convex Cover is \(\exists\mathbb{R}\)-hard.
In this paper, we provide the first constant-factor approximation for Convex Cover. The approximation factor is 6: that is, given any polygon \(P\), our algorithm will return a convex cover of \(P\) whose cardinality is at most six times that of the optimal cover. Moreover, our algorithm has a much more palatable runtime of (nearly) quadratic time.
En route, we also provide a constant-factor approximation algorithm with the same runtime for the Hidden Set problem - here, we want to maximize the number of points that we can place inside \(P\) which do not see each; see the example below:
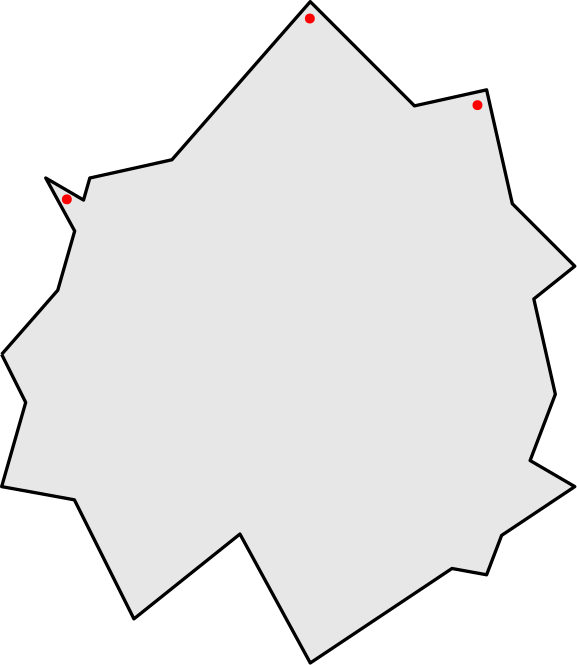An optimal hidden set of our polygon.
Our algorithm returns a hidden set whose size is at least an eighth of the optimal hidden set size. This is the first approximation algorithm for Hidden Set.
My coauthors for this work were Reilly Browne, Joe Mitchell, and Valentin Polischuk. This was published at FOCS 2023 (DOI). A longer version of the talk that Reilly presented at FOCS is available on his YouTube channel. Feel free to email me if you want to discuss this topic! The pre-print of this paper can be downloaded as a PDF from below: